color777x

급할 것 없어. 한 걸음씩 가자.

Python으로 해보는 수학: 중1. 소인수분해

1 분 소요

중학교 1학년 1단원 수와 연산

소인수분해는 초등 수학으로 거슬러 올라가서 약수, 소수, 합성수, 소인수의 개념으로부터 시작된다.

약수는 어떤 수를 나머지 없이 나눌 수 있는 정수이다. 소수는 약수가 1과 자신만으로 나누어 떨어지는 1보다 큰 양의 정수를 뜻하고, 합성수는 2개 이상의 약수를 가지고 있는 수이며, 소인수는 자연수의 약수 중 소수인 것을 소인수라고 부른다.

소인수분해는 합성수를 소인수로 분해하는 것이다.

이미지 설명소인수 분해 방법 [출처: ZUM 학습백과]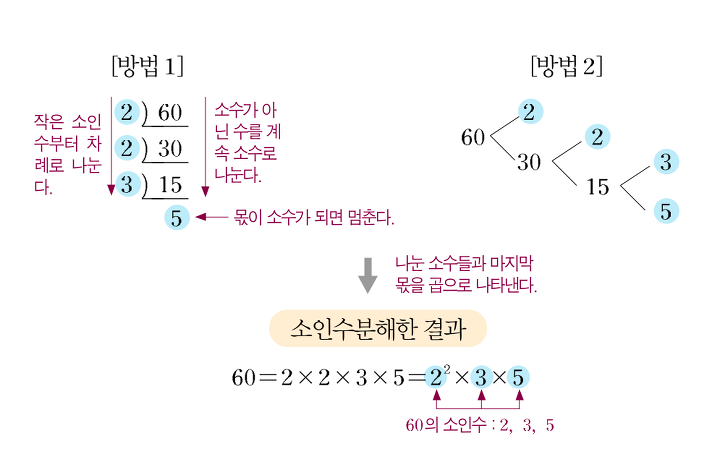

image-20210819051918420

  • 소인수분해를 Python으로 해보기

사실 아직 실력이 부족하여 여러 블로그를 참고하였다. ratsgo’s blog

# 특정 범위 내 숫자들 중 소수가 아닌 것을 거르는 과정을 반복하다보면 
# 결국 소수만 남게 된다고... [이를 에라토스테네스의 체라고... 처음들어본다.. ㅠㅠ]

# 에라토스테네스의 체...
import math
def primeSieve(sieveSize):
    # creating Sieve (0~n까지의 slot)
    sieve = [True] * (sieveSize+1)
    # 0과 1은 소수가 아니므로 제외
    sieve[0] = False
    sieve[1] = False
    # 2부터 (루트 n) + 1까지의 숫자를 탐색
    for i in range(2,int(math.sqrt(sieveSize))+1):
        # i가 소수가 아니면 pass
        if sieve[i] == False:
            continue
        # i가 소수라면 i*i~n까지 숫자 가운데 i의 배수를
        # 소수에서 제외
        for pointer in range(i**2, sieveSize+1, i):
            sieve[pointer] = False
    primes = []
    # sieve 리스트에서 True인 것이 소수이므로
    # True인 값의 인덱스를 결과로 저장
    for i in range(sieveSize+1):
        if sieve[i] == True:
            primes.append(i)
    return primes

# 소인수분해
def get_prime_factors(n):
    # n 범위 내의 소수를 구한다
    primelist = primeSieve(n)
    # 이 소수들 중 n으로 나누어 떨어지는
    # 소수를 구하고, 몇 번 나눌 수 있는지 계산
    # 예 : n = 8, factors = [(2, 3)]
    # 예 : n = 100, fcount = [(2: 2), (5: 2)]
    factors = []
    for p in primelist:
        count = 0
        while n % p == 0:
            n /= p
            count += 1
        if count > 0:
            factors.append((p, count))
    return factors

다른 방법도 알아볼까?

import math
N = int(input())
p=[]
if N == 1 :
    print("error")
while N !=1:
    if len(p)==0:
        start=2
    else:
        start=p[-1]
    for i in range(start,N+1):
        count = 0
        while N % i==0:
            #print(i)
            count += 1
            N=N//i
        if count:
            p.append((i, count))
print('x'.join(' %d^%d '%(e[0], e[1]) for e in p))

다음에는 실제로 소인수분해를 적용하는 암호학에 대해서 알아보아야겠다.

참고